Obsah:
- 1 Booleova algebra v programování
- 2 Logické funktory
- 3 Logické obvody
- 4 Názvosloví států
- 5 Logická hradla v digitálních obvodech
- 6 George Boole
- 7 Booleova algebra – principy
- 8 Typy logických hradel
- 9 Hradlo NOT
- 10 Hradlo AND
- 11 Hradlo NAND (-AND)
- 12 Hradlo OR
- 13 Hradlo NOR
- 14 Hradlo XOR (nebo EXOR)
- 15 Logické zákony
- 16 Logická hradla – Často kladené otázky
Logická hradla jsou nástroje, které jsou stavebními kameny strojů, automatů nebo robotů. Počítače, které dnes používáme, používají miliony logických mechanismů nazývaných digitální hradla (nebo logické brány). Jedná se o elektronické součástky, které na svých vstupech přijímají binární signály a vracejí hodnoty 1 nebo 0 – o- true nebo false.
Logická hradla jsou stálou součástí mnoha strojů. V dnešní době jsou to obvykle integrované obvody skládající se z řady vhodně zapojených tranzistorů. Podobného efektu lze dosáhnout například pomocí hydraulických nebo pneumatických zařízení. Zjednodušeně řečeno, princip hradel spočívá v použití jednoho ze dvou elektrických napětí (logických úrovní). Jedná se o napětí s hodnotami mezi 0 V a 0,8 V (úroveň 0 – false), zatímco druhá hodnota napětí by měla být mezi 2 V a 5 V (úroveň 1 – true). Rozlišení tohoto typu – s takovými hodnotami napětí – se používá v obvodech typu TTL (tranzistor-tranzistor-logika).

Booleova algebra v programování
Booleova algebra je typ algebraické struktury – pokud jste programátoři a nebyli jste s tímto pojmem přímo seznámeni, pravděpodobně rychle uhodnete, o co se jedná. Booleova algebra má širokou škálu aplikací. Mnoho programovacích jazyků používá tzv. booleovský typ (například booleovské proměnné nebo booleovské funkce, označované také jako logické funkce) – mimo jiné jazyky jako Pascal, C++, C#, PHP nebo Java. Booleovská proměnná nebo výsledek booleovské funkce může nabývat pouze jedné ze dvou hodnot – 0 nebo 1. Booleovský typ se používá k určení výsledku funkce (true nebo false) a k označení událostí “vlajkou” a používá se také jako podmínka pro podmíněný příkaz nebo například jako podmínka pro ukončení nebo pokračování cyklu.
Logické funktory
Označují se také jako funktory tvořící věty a jedná se o výraz, který spolu s argumenty funktoru, tj. dalšími výrazy, tvoří funkci věty neboli větu.
Booleova algebra – vzorce
[zdjęcie ukazujące wszystkie wzory Algebry Boole’a]
Logické obvody
Říká se jim také digitální obvody. Pracují s diskrétními hodnotami. Jsou vytvořeny na základě logických hradel, která provádějí základní logické operace, jako je součin, negace nebo součet.
Názvosloví států
Napěťové úrovně přímo odpovídají logickým hodnotám z Booleovy algebry. Logická úroveň rovná nule se často označuje písmenem F (od false, což z angličtiny znamená “nepravda”) nebo L (od low – což znamená “nízký”). Analogicky se úroveň rovná 1 často označuje písmenem T (od true– což znamená “pravdivý”) nebo H (od high – což znamená “vysoký”).
Logická hradla v digitálních obvodech
Uvnitř počítače neustále probíhají operace, při kterých počítač používá právě logická hradla – napěťové úrovně jsou ekvivalentem bitů. Logické hradlo na svém výstupu vrací odpovídající elektrické napětí, které opět spadá do výše definovaného rozsahu a označuje jeden ze dvou stavů (1 – true nebo 0 – false). Vyplývá to z logické funkce, kterou hradlo provádí (tj. například konjunkce, negace nebo alternativa). Logická hradla, která se používají v elektronice, jsou zařízení, která využívají vhodně zapojené elektronické součástky – jedná se především o tranzistory, kondenzátory, polovodičové diody a rezistory (odpory). Dnešní procesory se skládají z miliard velmi malých, vhodně zapojených tranzistorů. Ty jsou klíčem k fungování každého digitálního obvodu. Každý tranzistor má tři elektrody – source, drain a gate. Když se na poslední z nich přivede napětí, změní se vodivost kanálu. Tato znalost fungování tranzistorů je dostatečná pro dobré pochopení fungování logických hradel. Logická hradla si lze také jednoduše představit jako malé černé krabičky, na jejichž vstup se přivádí napětí tak, aby se na výstupu objevilo výsledné napětí závislé na funkci (vstupním signálu). Tento typ přístupu plně postačuje k návrhu i těch nejsložitějších digitálních sítí.
George Boole
Booleova algebra je typ algebraické struktury pojmenovaný po známém filozofovi, matematikovi a logikovi Georgi Booleovi. Díky zavedení konceptu Booleovy algebry je uznáván jako jeden ze zakladatelů matematické logiky a informatiky. Narodil se 2. listopadu 1815 v Lincolnu a žil až do roku 1859. Narodil se v rodině, kde byl jeho otec obuvníkem – ten ho chtěl poslat na dobrou školu, ale kvůli nedostatku dostatečných finančních prostředků tak nemohl učinit. Učil svého syna, co mohl, a přiměl ho, aby se učil latinsky, což byla tehdy jakási propustka do vyšších vrstev. George se učil z knih a jako dospívající začal učit na základních školách. Když mu bylo asi 20 let, seznámil se s pracemi Josepha Lagrange a Pierra Laplace a začal psát vlastní práce z matematiky. První z nich byly špatně zpracované, ale George bohužel neměl finanční prostředky na to, aby se na univerzitě zdokonalil.
Přesto se jeho práce stala natolik známou a významnou, že mu byla v roce 1844 udělena medaile Královské společnosti. Později – navzdory svému nedostatečnému formálnímu vzdělání – byl přijat na univerzitu jako profesor. V roce 1854 vydal své nejvýznamnější dílo s názvem“Zkoumání zákonů myšlení, na nichž jsou založeny matematické teorie logiky a pravděpodobnosti” (z angl: “An Investigation of the Laws of Thought, on which are founded the Mathematical Theories of LogicandProbabilities“). Přímo přispěl ke stavu dnešní digitální techniky – provoz milionů počítačů a zařízení po celém světě funguje tak, že se v nich využívají principy Booleovy algebry.

Booleova algebra – principy
Booleova algebra definuje následující základní zákony:
I – Zákon střídání sčítání a násobení. Znamená to, že výsledek výrazu a x b je ekvivalentní výsledku výrazu b x a (přičemž “x” označuje znaménko násobení). Mezi výrazy a + b a b + a lze umístit znaménko rovnosti.
II – Zákon spojitosti násobení. Znamená to, že výsledek a x b x c je stejný jako výsledek a(b x c) a (a x b)c. Stejný princip platí i pro sčítání – zákon spojitosti sčítání – výsledek výrazu a+b+c se rovná výsledku (a+b)+c a a+(b+c).
III – Zákon dělitelnosti násobení a sčítání. Výraz a(b+c) je ekvivalentní výrazu (a × b)+(a × c). Stejná situace platí opět pro sčítání vzhledem k násobení: výraz a + b × c je roven (a+b)×(a+c).
Typy logických hradel
Činnost logických hradel lze snadno rozčlenit pomocí tzv. pravdivostních tabulek. Ty popisují postupné kombinace vstupních stavů a odpovídající stavy na výstupu hradla.
Hradlo NOT
Z hlediska činnosti je hradlo NOT nejjednodušší ze všech zde popsaných (a obecně ze všech používaných logických hradel). Jeho činnost je založena na negaci (inverzi) signálu, který dostává na vstup. V praxi to vypadá následovně: Pokud je na vstup přiveden signál o hodnotě 1 (true), na výstup se přivede signál o hodnotě 0 (false). A naopak, pokud je na vstup přiveden signál o hodnotě 0, na výstup bude přivedena 1.
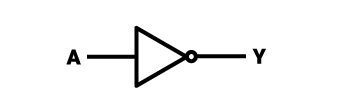
Příklad 1:
vstup = 1
výstup = 0
Příklad 2
vstup = 0
výstup = 1
Hradlo NOT je také znázorněno grafickým symbolem – jedná se o rovnoramenný trojúhelník, který lze také vidět jako šipku směřující doprava – v místě, kde se protínají delší ramena, je k jeho vrcholu tečna kružnice (její průměr je přibližně ¼ délky kratší strany trojúhelníku). Vstup do brány je vlevo od grafického zobrazení (kolmo na kratší rameno trojúhelníku), zatímco výstup je vpravo od symbolu (za popisovaným kruhem). Brána má pouze jeden vstup a jeden výstup. Příklad integrovaného obvodu (TTL), který obsahuje 6 takovýchto hradel (NOT), se nazývá “7404”.
Hradlo AND
Při činnosti logického hradla AND lze výsledek 1 získat pouze tehdy, pokud se oba vstupy rovnají jedničce. Tento typ hradla může být ve třívstupové, čtyřvstupové a mnohem vícevstupové verzi. Všimněte si, že nezáleží na tom, kolik vstupů je ve vysokém stavu – vysoký stav na výstupu bude možný pouze tehdy, pokud bude na každém vstupu logická jednička.
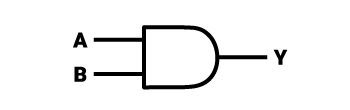
Příklad 1:
vstup 1 = 1
vstup 2 = 0
vstup 3 = 1
výstup = 0
Příklad 2:
vstup 1 = 1
vstup 2 = 1
vstup 3 = 1
výstup = 1
Logický symbol hradla AND připomíná obrazec složený ze čtverce a poloviny kruhu (rozříznutého podél průměru, jehož délka je rovna délce strany čtverce. Pravá strana čtverce je spojená s plochou částí půlkruhu. Celek připomíná šíp s vyhlazeným hrotem, který směřuje doprava. Na jeho levé straně jsou umístěny vstupy hradla na levé straně čtverce a výstup analogický symbolu hradla NOT je na pravé straně. Příklad integrovaného obvodu (TTL), který obsahuje 4 taková hradla (hradla AND se dvěma vstupy), se nazývá “7408”.
Hradlo NAND (-AND)
Činnost hradla NAND (-AND) je přesně opačná než u hradla AND. Alternativním názvem pro hradlo NAND je výraz “-AND”. – Pomlčka před AND znamená negaci. Takto lze také interpretovat činnost hradla NAND – je to přesně tak, jako kdyby se na vstup hradla AND vložily příslušné hodnoty, výsledek se objevil na jeho výstupu a pak prošel ještě hradlem NOT. Činnost hradla NAND je také možné interpretovat tak, jako by před každým vstupem hradla AND bylo hradlo NOT. Zjednodušeně lze činnost hradla NAND popsat takto – nízký stav (0) se objeví pouze tehdy, pokud se na všech vstupech objeví vysoký stav (1). Je třeba poznamenat, že hradlo NAND má neomezený počet vstupů.
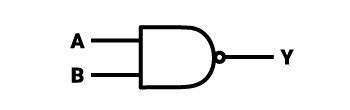
Příklad 1:
vstup 1 = 1
vstup 2 = 0
vstup 3 = 1
výstup = 1
Příklad 2:
vstup 1 = 1
vstup 2 = 1
vstup 3 = 1
výstup = 0
Logický symbol hradla NAND je téměř stejný jako u hradla AND. Je to čtverec, na jehož pravé straně je připojena polovina kruhu – řez podél průměru, jehož vrcholy se setkávají s vrcholy čtverce. Celek připomíná šipku s vyhlazeným hrotem, na jejímž konci je malý kruh o délce asi ¼ strany čtverce, jehož průměr je prodloužením poloměru půlkruhu a je v polovině výšky celého obrázku. Kruh je stejný jako ten, který byl popsán u hradla NOT – znamená přesnou inverzi symbolu, vedle kterého se nachází (trojúhelník je symbolem pro součet – inverzí je negace, AND je negací NAND). Vstupy hradla jsou umístěny na levé straně čtverce, zatímco výstup se nachází hned za malým kolečkem. Příklad integrovaného obvodu (TTL), který obsahuje 4 taková hradla (hradla NAND se dvěma vstupy), se nazývá “7400”, “7401” a “7403”.
Hradlo OR
Na výstupu hradla OR se vždy objeví výsledek 1, pokud je alespoň jeden ze vstupů ve stavu vysoký. To také znamená, že pokud je více než jeden vstup ve vysokém stavu, objeví se jednička i na výstupu. Nula se tedy na výstupu objeví pouze tehdy, pokud jsou všechny vstupy hradla rovněž nastaveny na nulu. Výstup je samozřejmě vždy jen jeden. Typický obvod obsahuje dva vstupy, ale může mít nekonečný počet vstupů a bude fungovat stejně.
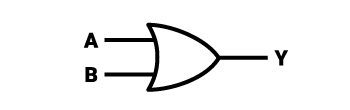
Příklad 1:
vstup 1 = 0
vstup 2 = 1
vstup 3 = 0
výstup = 1
Příklad 2:
vstup 1 = 1
vstup 2 = 1
vstup 3 = 1
výstup = 1
Příklad 3:
vstup 1 = 0
vstup 2 = 0
vstup 3 = 0
výstup = 0
Logický symbol pro hradlo OR opět připomíná šipku. Určitě vidíte podobnost se symbolem pro logická hradla AND a NAND, ale bude jednodušší popsat ho od začátku. Symbol hradla OR lze popsat jako obrázek, který se skládá ze spojitého čtverce a rovnoramenného trojúhelníku, jehož délka nejkratší strany je rovna výšce strany čtverce, k jehož pravé straně dotyčný trojúhelník přiléhá. Levá strana čtverce je vyříznutá a prostor za výřezem má tvar oblouku, který je fragmentem tečné kružnice o průměru několikanásobně větším, než je strana čtverce. Obě ramena připojeného rovnoramenného trojúhelníku jsou na vnější straně vypouklá, čímž se celek zefektivní, ale zároveň zůstane zachován ostrý konec “šípu”. Konvexitu lze definovat tak, že styčné stejné strany trojúhelníku jsou dvě kruhové výseče o průměru několikanásobně větším než kterákoli strana trojúhelníku. Příkladem integrovaného obvodu (TTL), který obsahuje 4 taková hradla, je “7432”.
Hradlo NOR
Analogicky k výše uvedeným hradlům lze odhadnout, jaký druh operace představuje hradlo NOR. Při přezkoumání předchozích názvů si lze všimnout trendu: hradla, jejichž názvu předchází písmeno N, budou pracovat přesně opačně než jejich originál. Je to proto, že písmeno N (od not, což znamená “ne”) znamená negaci (stejně jako u AND a NAND). Činnost hradla NOR lze popsat jako úplný opak činnosti hradla OR – můžete se na něj dívat tak, že postupně působí jako hradlo OR na všechny vstupní signály, které přijalo, a pak vloží svůj výstupní signál na vstup hradla NOT – výsledek bude znamenat, že funguje hradlo NOR. Samozřejmě lze také předpokládat, že před každým vstupem hradla OR bude použito hradlo NOT – v takovém případě bude každý vstup hradla OR pocházet z výstupu hradel NOT. Zjednodušíme-li popis principu činnosti, hradlo NOR bude na svém výstupu vždy vracet nízký stav, kromě případů, kdy jsou všechny stavy nastaveny na 0. Taková hradla mohou mít nekonečný počet vstupů.
Příklad 1:
vstup 1 = 1
vstup 2 = 0
vstup 3 = 1
výstup = 0
Příklad 2:
vstup 1 = 0
vstup 2 = 0
vstup 3 = 0
výstup = 1
Příklad 3:
vstup 1 = 1
vstup 2 = 0
vstup 3 = 0
výstup = 0
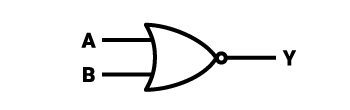
Grafický symbol pro takové logické hradlo je opět analogický změnám vzhledu, které nastaly mezi symboly logických hradel a symboly logických hradel, které byly inverzní k těm prvním. Prototyp negační verze symbolu zachovává na pravém konci malý kruh s průměrem, jehož délka se blíží ¼ výšky celého grafického symbolu. V tomto případě se jedná o dříve popsaný čtverec, jehož levá strana je mírně odsazená – tvar odsazení vypadá jako malý výřez kruhu o několikanásobku průměru strany čtverce. Pravá strana čtverce sousedí s rovnoramenným trojúhelníkem, jehož strany jsou zaoblené – jemně překryté výřezem kruhu o velmi velkém průměru. K ostrému konci vpravo přiléhá malé kolečko – grafický znak označující negaci. Vlevo jsou vstupy logického hradla (na straně výřezu čtverce) a za malým kruhem je výstup hradla. Celé to vypadá jako nějaký druh náboje. Příklad integrovaného obvodu (TTL), který obsahuje 4 taková hradla, se nazývá “7402”.
Hradlo XOR (nebo EXOR)
Hradlo EXOR (Exclusive-OR, což znamená “výhradně ne”) je jednou z unikátních funkcí, která již nepatří do skupiny nejběžnějších – základních logických hradel. Jedná se o hradlo, které má na svém vstupu vždy přesně dvě proměnné (je to funkce dvou proměnných). Získává vysoký stav vždy, pokud je pouze jeden ze vstupních stavů roven logické jedničce. Nízký stav na výstupu nastane, pokud jsou obě vstupní hodnoty rovny. Hradlo XOR provádí operaci bitového sčítání modulo-2.
Příklad 1:
vstup 1 = 1
vstup 2 = 1
výstup = 0
Příklad 2:
vstup 1 = 0
vstup 2 = 0
výstup = 0
Příklad 3:
vstup 1 = 1
vstup 2 = 0
výstup = 1
Příklad 4:
vstup 1 = 0
vstup 2 = 1
výstup = 1
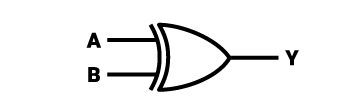
Grafické znázornění logického hradla XOR je symbol, který vypadá podobně jako grafické znázornění logického hradla OR. Hradlo XOR zjednodušeně vypadá jako náboj, ale navíc má čáru rovnoběžnou s levou stranou symbolu. Levá strana symbolu je bývalá stěna čtverce, která je konkávní díky výřezu ve tvaru kruhového výseku s velmi velkým poloměrem. Již dříve popsaná rovnoběžná čára umístěná vlevo od symbolu má tvar kruhového výseče o stejném poloměru, jaký má kruh, jehož výseč byla z levé strany čtverce vyříznuta.
Logické zákony
Jsou to věty, které jsou pravdivé při jakékoli interpretaci mimologických konstant, které obsahují. Logický součet je logická věta, nazývaná také alternativou, ve tvaru p nebo q.
Logická hradla – Často kladené otázky
Jak hodnotíte tento článek na blogu?
Klikněte na hvězdičku a ohodnoťte!
Průměrné hodnocení 4.5 / 5. Počet hlasů 46
Zatím nejsou žádné hlasy! Buďte první, kdo ohodnotí tento článek.





















