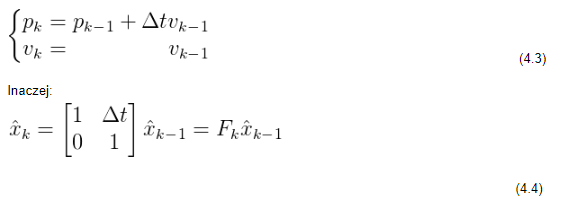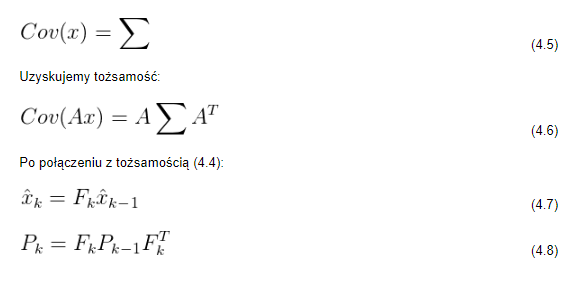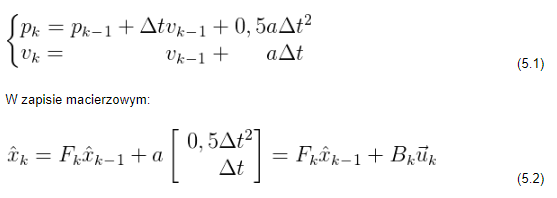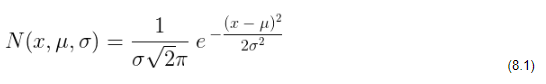Kalmanův filtr – teoretické základy

Široká škála technických věd potřebuje k popisu nejrůznějších jevů vhodné matematické nástroje. Jak automatizace, tak robotika, teorie řízení a řídicích systémů, elektronika, elektroakustika, číslicové zpracování signálů a příbuzné obory jsou založeny na lineární algebře, operátorovém kalkulu, genetických algoritmech, numerických metodách, ale i fuzzy logice a dalších odvětvích matematiky. Vedle matematických nástrojů oblíbených v technických vědách, jako je Laplaceova transformace, Z-transformace nebo metoda konečných prvků, algoritmus, který způsobil revoluci mj. Jedná se o jeden z klasických nástrojů odhadu. Je to jeden z klasických nástrojů odhadu, který se používá v aplikacích, jako je zpracování signálů, řízení elektrických pohonů, autonomní systémy řízení vozidel a řízení procesorů v počítačích. V odborné literatuře je Kalmanův filtr většinou popisován v konkrétních aplikačních případech, jako jsou autonomní roboty nebo lineární systémy automatického řízení s Gaussovsky rozloženým šumem, což velmi znesnadňuje přehledné představení problematiky po základní stránce. Náš článek popisuje diskrétní Kalmanův filtr pomocí vektorového a maticového počtu a ilustruje praktický příklad jeho použití.

Co je Kalmanův filtr?

Kalmanův filtr je speciální algoritmus, který byl vyvinut a demonstrován na počátku 60. let XX. století. Rudolf Emil Kalman (1930-2016) – maďarsko-americký elektroinženýr. Kalmanův filtr lze použít v jakékoli aplikaci, kde je snížená spolehlivost informací o parametrech dynamických systémů. Parametry dynamických systémů. Pak můžeme také předvídat, jaké události mohou nastat příště. To se provádí na základě dosud získaných informací. V úvahu se pak bere mnoho podmíněných faktorů, které se mohou měnit a mít významný vliv na výsledek automatizačního systému, v němž je Kalmanův filtr implementován. Tento algoritmus je vynikající pro dynamické systémy, jejichž parametry se průběžně mění a ke správné funkci nepotřebují velké množství paměti, pouze stav systému předcházející dalšímu. Důležitým faktorem ve prospěch tohoto algoritmu je jeho vysoká rychlost, díky níž je úspěšně implementován v aplikacích reálného času a vestavných systémech.

Kalmanův filtr – v jakých aplikacích se vyplatí jej použít?

Než si ukážeme algoritmus, který ukazuje princip Kalmanova filtru, použijeme jeden hardwarový příklad jeho použití, kterým je robot, který se dokáže pohybovat v hustě zalesněných oblastech. Aby vestavěný navigační systém správně fungoval, potřebuje znát svou přesnou polohu.

Můžeme tedy říci, že náš robot je definován stavovou proměnnou xk, , která je definována vektorem o dvou složkách – poloze p  a rychlosti v:

(3.1)

Stav systému je určen číselnými údaji, které definují jeho základní konfiguraci, a mohou to být číselné údaje pro libovolné veličiny. V našem případě jsou těmito veličinami poloha a rychlost, ale u jiných systémů to může být také zbývající množství paliva v nádrži v automobilu, teplota hrotu v baňce pájecí stanice, proud v budicím obvodu synchronního generátoru a mnoho dalších parametrů, které v závislosti na aplikaci vyžadují sledování hodnot. Robot v prezentovaném příkladu je vybaven navigačním systémem GPS, který je schopen určit jeho souřadnice s přesností na deset metrů. To je uspokojivý výsledek, ale vzhledem k proměnlivosti různých parametrů terénu, po němž se robot pohybuje, je nutné, aby vestavěný systém GPS byl ještě přesnější. V nejhorším případě by robot s přesností souřadnic na deset metrů mohl dokonce spadnout do propasti.

Pro přesné určení dráhy robota je nutné znát parametry jednotlivých signálů ovládajících jeho pohonnou jednotku – systém GPS pak “ví”, že když se robot pohybuje tak, že vykoná téměř přímočarý pohyb, je pravděpodobné, že se bude v dalším kroku pohybovat stejným způsobem a stejným směrem. Robot však stále nebude dostávat informace o okolních faktorech, které mohou ovlivnit jeho pohyb. Robot však stále nepřijímá informace o faktorech prostředí, které mohou ovlivnit jeho pohyb, např. poryvy větru, kluzká půda, a také nerovnosti terénu a překážky na silnici, které dříve nepředvídal (např. ležící větve stromů). Pak může počet otáček provedených silničními koly robota nesprávně reprezentovat jeho pohyb, což vede k nesprávné předpovědi dalšího kroku popisujícího pohyb robota.

Senzory GPS poskytují nepřímé informace o stavu systému (robota), ale s omezenou přesností. Senzory GPS poskytují nepřímé informace o stavu systému (robota), ale s omezenou přesností. Nicméně se ukazuje, že údaje získané ze senzorů GPS lze využít v procesu odhadu k získání souřadnicových měření se zvýšenou přesností. Právě to umožňuje algoritmus tzv. Zde přichází ke slovu algoritmus známý jako Kalmanův filtr.

Kalmanův filtr – začátek algoritmu

Pro zahájení algoritmu Kalmanova filtru zapišme rovnici stavového vektoru (3.1) v maticovém tvaru:

(3.2)

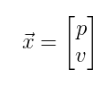
Aktuální polohu a rychlost objektu neznáme, protože existuje konečná množina zahrnující celou škálu možných kombinací polohy a rychlosti, které se mohou ukázat jako odpovídající skutečnosti, ale mezi nimi jsou i takové, které více či méně odpovídají skutečným hodnotám. Algoritmus Kalmanova filtru předpokládá, že obě stavové proměnné (ve zkoumaném případě jsou to poloha a rychlost objektu) jsou rozděleny podle Gaussova rozdělení (normální rozdělení). Každá proměnná má střední hodnotu, která se nachází ve střední poloze náhodného rozdělení a je zároveň očekávanou hodnotou, a rozptyl, který definuje nejistotu měření. Na první pohled poloha a rychlost objektu spolu nesouvisí, což znamená, že informace o stavu jedné proměnné (složky stavového vektoru) nebude dostatečná k určení druhé proměnné. Ve skutečnosti poloha a rychlost objektu spolu souvisejí, tj. pravděpodobnost pozorování určité hodnoty proměnné, která určuje polohu objektu, závisí na jeho rychlosti.

Tato situace může nastat například tehdy, když známe předchozí polohu objektu a snažíme se určit jeho aktuální polohu. Pokud je rychlost objektu příliš vysoká, pak další měření polohy objektu bude vzdálenější. Pokud se naopak objekt pohybuje nižší rychlostí, pak měření polohy ve srovnání s předchozím měřením ukáže posunutí objektu o menší vzdálenost než při vyšší rychlosti. Vztah mezi polohou a rychlostí objektu je při sledování objektu velmi důležitý, protože poskytuje cenné informace – měření jednoho parametru usměrňuje potenciální výsledky následných měření stejných parametrů. To je hlavní účel algoritmu Kalmanova filtru – shromáždit co nejvíce údajů zatížených nepřesností měření, aby bylo možné získat co nejpřesnější výsledek měření. Vztah mezi stavovými proměnnými je definován kovarianční maticí a každým prvkem v ní obsaženým. Pak prvek určuje stupeň korelace mezi i-tou stavovou proměnnou a j-tou stavovou proměnnou, přičemž kovarianční matice je čtvercová matice, tj. její počet řádků je stejný jako počet sloupců.

Maticový zápis

Pro modelování stavu objektu je užitečné použít maticový zápis s využitím Gaussovy fuzzyfikace – pro určení stavu objektu pro k-té měření pak potřebujeme dvě rovnice. xk je vektor středních (skalárních) hodnot, což jsou očekávané hodnoty, a Pro modelování stavu objektu je užitečné použít maticový zápis s využitím Gaussovy fuzzyfikace – pro určení stavu objektu pro k-té měření pak potřebujeme dvě rovnice. _.xk je vektor středních (skalárních) hodnot, což jsou očekávané hodnoty, a P_k je kovarianční matice.

V tomto případě jsou stavovými proměnnými poloha a rychlost objektu, ale je třeba poznamenat, že stav může být popsán libovolným počtem proměnných reprezentujících libovolné parametry. Pak je nutné zaznamenat hodnoty proměnných pro současný stav (v čase k-1), aby bylo možné přistoupit k předpovědi hodnot pro stav v čase k. Není známo, který stav odráží skutečné parametry objektu, ale to je pro proces predikce irelevantní. Fázi predikce lze vizualizovat pomocí vektoru F_k. Každý bod, který se nachází ve stavovém prostoru v aktuálním kroku, se přesune do nové oblasti – oblasti předpovídaných hodnot, do které se systém přesune, pokud byl předchozí stavový prostor správně lokalizován. K nalezení předpovídaného stavového prostoru při znalosti aktuálních hodnot stavových veličin určujících polohu a rychlost použijeme soustavu rovnic:

Tímto způsobem získáme predikční matici, která obsahuje informace o dalším (po k-1) stavu (k). Nicméně stále není jasné, jak správně aktualizovat kovarianční matici. Zde je třeba každý bod obsažený v rozdělení vynásobit maticí A:

Vliv vnějších faktorů

V této fázi ještě nebyly zohledněny všechny faktory, a to faktory, které přímo nesouvisejí s vlastnostmi zkoumaného systému, ale vyskytují se nezávisle, ale mohou stav systému také ovlivnit. Například je-li objektem popsaným stavovými proměnnými elektrická lokomotiva (elektrická lokomotiva) – když strojvedoucí zvýší napájecí napětí motorů, např. snížením magnetického toku v budicím obvodu, lokomotiva zrychlí. Podobně v popsaném případě robota může palubní navigační systém narazit na problémy při přenosu signálu do řídicího systému robota, aby otočil kola nebo zastavil, např. když hrozí, že robota za jízdy převrátí vítr. Znalost těchto dodatečných informací o vnějších podmínkách lze zohlednit pomocí vektoru

_k, což umožňuje zahrnout korekci do predikční matice:

Za předpokladu, že na základě řídicích signálů (např. plnícího faktoru řídicího signálu otáček motoru) známe očekávanou hodnotu zrychlení a, získáme soustavu rovnic:

_k je řídicí vektor – v jednoduchých systémech bez vnějších vlivů lze tyto složky zanedbat. Co když ale předpovězené řešení přesto není dostatečně přesné?

Vnější nejistota

Celý proces predikce plynule pokračuje, pokud je stav objektu založen na všech zohledňovaných faktorech, včetně vnějších faktorů, jejichž výskyt nesouvisí s vlastnostmi samotného systému, které ovlivňují. To platí tak dlouho, dokud známe maximální parametry vnějších faktorů, vůči nimž bude systém odolný. Ale co když se objeví faktory, o kterých nevíme? Například drony (stejně jako jiná letadla) podléhají poryvům větru, které mohou narušit dráhu letu, a dokonce způsobit srážku s blízkým objektem (například stromem). Robot na kolečkách může při jízdě uklouznout, což má za následek, že se nemůže pohybovat dál, přestože se kola otáčejí. Pak, protože tyto faktory nejsou brány v úvahu, může algoritmus ve fázi předpovědi selhat, což může mít za následek i nenapravitelné poškození systému.

Aby se zvýšila pravděpodobnost těchto vysoce nežádoucích účinků, musí být do výpočtu pro každý krok předpovědi zahrnuta další nejistota. V původním odhadu je pak původní odhad rozšířen o řadu stavů. Předpovídané řešení x_k-1, se přesune do kovarianční oblasti Q_k. Jinými slovy lze také říci, že vnější faktory, které jsou zdrojem dodatečné nejistoty, tvoří šum kovarianční matice Q_k. Výsledkem takového působení je nová Gaussova šmouha, která má jinou kovarianci vzhledem k původní Gaussově šmouze, ale stejnou očekávanou hodnotu stavové proměnné. Pak se získá rozšířená kovarianční matice zahrnutím faktoru Q_k:

Jinými slovy, aktualizovaná “nejlepší” očekávaná hodnota se předpovídá z předchozí očekávané hodnoty s přihlédnutím k vlivu vnějších podmínek. Také nově odvozená vnější nejistota, je výsledkem kombinace dříve vypočtené vnější nejistoty s rozšířenou nejistotou v důsledku vlivu vnějších podmínek. V této fázi můžeme dále zpracovávat data z měřicích senzorů.

Aproximace odhadu na základě měření

Testovaný systém může být vybaven několika měřicími senzory, které poskytují informace potřebné k určení jeho stavu. Ať už tyto senzory reagují na jakékoliv podněty, poskytují informace potřebné k určení polohy a rychlosti robota, takže se pomocí nich provádí nepřímá měření. Je důležité si uvědomit, že může dojít k nesouladu mezi jednotkami a měřítkem odečtu a jednotkami a měřítkem sledovaného stavu. Proto je popis snímačů modelován pomocí matice H_k. Rozložení odečtů ze snímačů lze předpovědět z rovnic:

Jednou z největších výhod algoritmu Kalmanova filtru je, že je imunní vůči nepřesnosti měření prováděných senzory (v důsledku šumu). Senzory mohou být nespolehlivé, což má za následek, že jakýkoli odhadovaný stav systému může být výsledkem řady parametrů snímaných senzory. Kalmanův filtr tento problém kompenzuje na minimum. Z každého pozorovaného údaje ze snímače můžeme usuzovat, že testovaný systém byl v přesně definovaném stavu. Vzhledem k přítomnosti nejistoty měření však může být několik předpovídaných stavů v rámci rozsahu odečtů senzorů pravděpodobnějších než jiné. Za tímto účelem zavedeme kovarianční matici neurčitosti R_k, která je výsledkem šumu vneseného senzory, a vektor průměrných pozorovaných údajů _k .
W ten sposób uzyskujemy dwa obszary rozmycia Gaussa – pierwszy wynikający z przewidywanego odczytu, a drugi z rzeczywistego odczytu z czujników.
Dzięki temu obszar poszukiwań optymalnego rozwiązania znacząco zawęża się i cały algorytm można wykonać od nowa w ten sam sposób, uzyskując jeszcze bardziej dokładne, tzn, jeszcze bardziej zgodne z rzeczywistością wyniki obliczeń na podstawie uzyskanych wcześniej danych pomiarowych.

Kalmanovo vylepšení

Pro určení matice definující Kalmanovo zesílení je nutné použít jednorozměrnou Gaussovu křivku s ohledem na 2 a střední hodnotu:

Vzájemným vynásobením rovnic křivek představujících normální rozdělení pro předpovídaný stav a skutečný stav zjištěný z údajů odečtených z měřicích senzorů získáme novou rovnici křivky, jejíž rozdělení zužuje rozsah hodnot pro vektor požadovaného stavu:

Pomocí maticového zápisu získáme:

kde K je matice definující Kalmanův zesílení.

Konečné výpočty

Na základě Gaussova rozdělení získáme dvě rozdělení. První získáme z předpovězeného měření (9.1) a druhé z pozorovaného měření.

Ze soustavy rovnic (9.3) určíme podmínky definující společnou plochu rozdělení (9.1) a (9.2).

V závislosti na potřebách aplikace lze celý algoritmus několikrát opakovat, aby se dosáhlo ještě přesnějších výsledků.